1. マンデルブロ集合の計算を高速化してみる
[概要]
有名なマンデルブロ集合の計算を JIT(numba) を使って高速化してみます。
[環境]
| 言語 : | Python, | 3.10.7 |
| ライブラリ: | numba, | 0.60.0 |
| OS : | Windows11 home, | 23H2 |
[手順]
高速化する元の Python ソースコードに下記2つを追加します。
(1) from numba import jit を追加します
(2) 高速化したい関数の前に @jit(nopython=True) を追加します。
[結果]
私のパソコンで動作させた場合の実行時間比較を下記表に記載します。
単純比較で 約30倍 高速になりました。
| 条件 | 実行時間 [秒] |
|---|---|
| 高速化前 | 27.2 |
| JIT(numba) 適用後 | 1.2 |
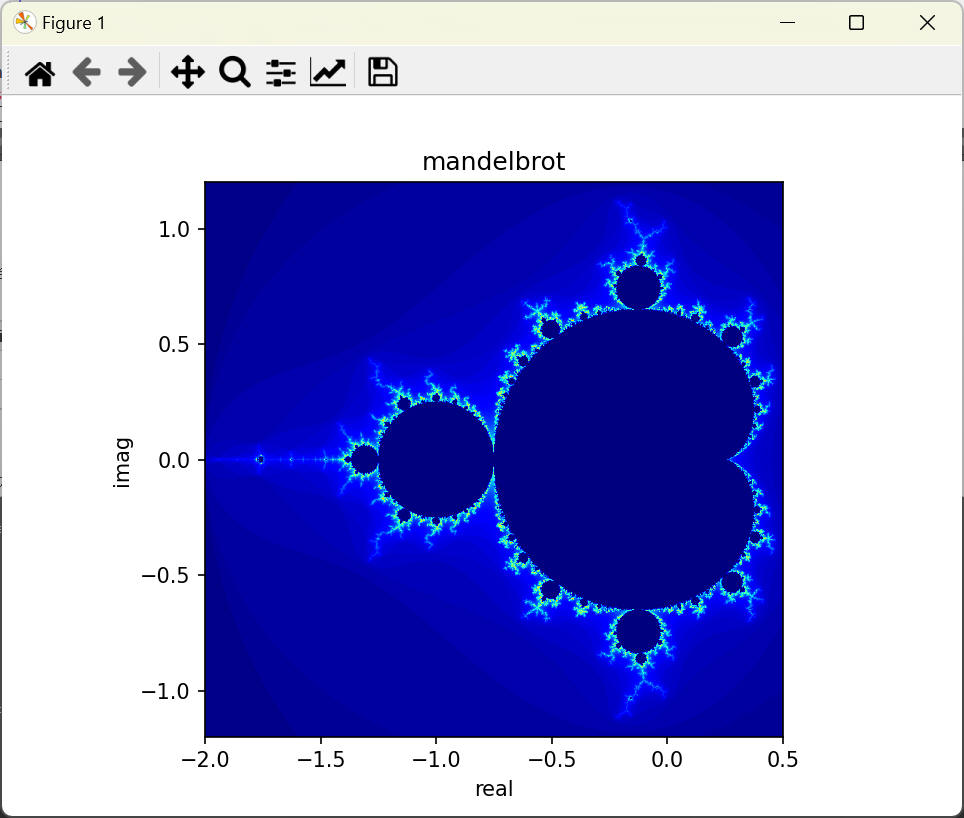
図. マンデルブロ集合 演算結果
[JIT(numba) による高速化後のソースコード]
''' マンデルブロ集合の画像を作成する 参考: 日経ソフトウェア 2021年7月号「特集1 Pythonプログラムを高速化!」 libraries: - matplotlib : pip install matplotlib - numba : pip install numba ''' from numba import jit # (1) import numpy as np from matplotlib import pyplot as plt from matplotlib.colors import Normalize import time STEP_COUNT = 100 MESH = 1000 REAL_MIN = -2 REAL_MAX = 0.5 IMAG_MIN = -1.2 #IMAG_MIN = -0.8 IMAG_MAX = 1.2 @jit(nopython=True) # (2) def check_mandelbrot(c): z = complex(0, 0) n = 0 while np.abs(z) <= 2 and n < STEP_COUNT: z = z ** 2 + c n += 1 return n ''' 概要: マンデルブロー集合を計算する ''' def create_mandelbrot_data(): real, imag = np.meshgrid( np.linspace(REAL_MIN, REAL_MAX, MESH), np.linspace(IMAG_MIN, IMAG_MAX, MESH)) length = len(real.ravel()) mandelbrot_data = np.zeros(length) for i in range(length): c = complex(real.ravel()[i], imag.ravel()[i]) n = check_mandelbrot(c) if n < STEP_COUNT: mandelbrot_data[i] = n mandelbrot_data = np.reshape(mandelbrot_data, real.shape) return mandelbrot_data ''' 概要: マンデルブロー画像を表示、JPEG画像として保存、をする ''' def create_jpg(mandelbrot_data): # imshow で画像が上限反転するので、先にデータを反転させる mandelbrot_data = mandelbrot_data[::-1] # 左右反転させる場合はこんな感じで書く #for i in range(len(mandelbrot_data)): # mandelbrot_data[i] = mandelbrot_data[i][::-1] fig = plt.figure() # サブプロット領域を作成。"111" = "1,1,1"。あまり気にしなくてよい。 # (FYI) https://qiita.com/kenichiro_nishioka/items/8e307e164a4e0a279734 ax = fig.add_subplot(111) # 軸ラベルを追加 ax.set_title('mandelbrot') ax.set_xlabel('real') ax.set_ylabel('imag') # 画像作成 ax.imshow(mandelbrot_data, cmap='jet', norm=Normalize(vmin=0, vmax=STEP_COUNT), extent=[REAL_MIN, REAL_MAX, IMAG_MIN, IMAG_MAX]) # JPEG画像保存 plt.savefig("mandelbrot.jpg") # 画像を表示 plt.show() # tight_layout() メソッドはサブプロット間の正しい間隔を自動的に維持します。 # (ここでは1つのグラフのみを表示するので意味はないかもしれません...。参照元の記載がこうなっていたので記載しています。) plt.tight_layout() plt.close() def main(): start = time.perf_counter() # 計測開始 mandelbrot_data = create_mandelbrot_data() end = time.perf_counter() # 計測終了 print('{:.1f} sec'.format(end-start)) create_jpg(mandelbrot_data) if __name__ == "__main__": main()
[高速化前のソースコード]
'''
マンデルブロ集合の画像を作成する
参考: 日経ソフトウェア 2021年7月号「特集1 Pythonプログラムを高速化!」
libraries:
- matplotlib : pip install matplotlib
'''
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.colors import Normalize
import time
STEP_COUNT = 100
MESH = 1000
REAL_MIN = -2
REAL_MAX = 0.5
IMAG_MIN = -1.2
#IMAG_MIN = -0.8
IMAG_MAX = 1.2
def check_mandelbrot(c):
z = complex(0, 0)
n = 0
while np.abs(z) <= 2 and n < STEP_COUNT:
z = z ** 2 + c
n += 1
return n
'''
概要: マンデルブロー集合を計算する
'''
def create_mandelbrot_data():
real, imag = np.meshgrid(
np.linspace(REAL_MIN, REAL_MAX, MESH),
np.linspace(IMAG_MIN, IMAG_MAX, MESH))
length = len(real.ravel())
mandelbrot_data = np.zeros(length)
for i in range(length):
c = complex(real.ravel()[i], imag.ravel()[i])
n = check_mandelbrot(c)
if n < STEP_COUNT:
mandelbrot_data[i] = n
mandelbrot_data = np.reshape(mandelbrot_data, real.shape)
return mandelbrot_data
'''
概要: マンデルブロー画像を表示、JPEG画像として保存、をする
'''
def create_jpg(mandelbrot_data):
# imshow で画像が上限反転するので、先にデータを反転させる
mandelbrot_data = mandelbrot_data[::-1]
# 左右反転させる場合はこんな感じで書く
#for i in range(len(mandelbrot_data)):
# mandelbrot_data[i] = mandelbrot_data[i][::-1]
fig = plt.figure()
# サブプロット領域を作成。"111" = "1,1,1"。あまり気にしなくてよい。
# (FYI) https://qiita.com/kenichiro_nishioka/items/8e307e164a4e0a279734
ax = fig.add_subplot(111)
# 軸ラベルを追加
ax.set_title('mandelbrot')
ax.set_xlabel('real')
ax.set_ylabel('imag')
# 画像作成
ax.imshow(mandelbrot_data, cmap='jet', norm=Normalize(vmin=0, vmax=STEP_COUNT), extent=[REAL_MIN, REAL_MAX, IMAG_MIN, IMAG_MAX])
# JPEG画像保存
plt.savefig("mandelbrot.jpg")
# 画像を表示
plt.show()
# tight_layout() メソッドはサブプロット間の正しい間隔を自動的に維持します。
# (ここでは1つのグラフのみを表示するので意味はないかもしれません...。参照元の記載がこうなっていたので記載しています。)
plt.tight_layout()
plt.close()
def main():
start = time.perf_counter() # 計測開始
mandelbrot_data = create_mandelbrot_data()
end = time.perf_counter() # 計測終了
print('{:.1f} sec'.format(end-start))
create_jpg(mandelbrot_data)
if __name__ == "__main__":
main()